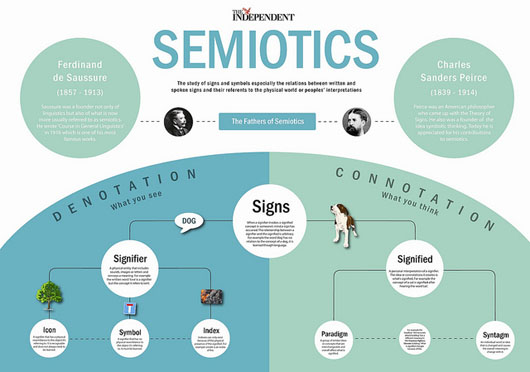
Semiotics
EXAMPLE: $a$ names $99$
$a$ is the name. $99$ is the thing.
Observe that $1$ and $99$ are themselves names.
What thing does $1$ name?
Observe that a name is itself a thing, and so may itself be named.
EXAMPLE: $a$ names $99$
$a$ is the name. $99$ is the thing.
If I tell you I have $a$ pencils, how many pencils have I told you that I have? I have 99 pencils.
EXAMPLE: 1, 2, 3, ... names the [set of all] natural numbers
'1, 2, 3, ...' is the name. 'the [set of all] natural numbers' are the several things.
In fact, '1, 2, 3, ...' is a convention for how to name all the counting numbers from 1 to infinity.
How do you say "1, 2, 3 ..."?
You may say "one, two, three and so on [forever]", or you may say "the [set of all] natural numbers, or you may say "all the counting numbers from one to infinity".
All these are synonymous. Do you see that a name may name another name, that many names may name the same thing (or name), and that many names may name the same [several] things (or names)?